Differences between revisions 5 and 6
⇤ ← Revision 5 as of 2011-08-03 11:00:47 →
Size: 1640
Editor: localhost
Comment: converted to 1.6 markup
← Revision 6 as of 2011-09-07 16:42:21 → ⇥
Size: 1646
Editor: 211
Comment:
Deletions are marked like this. Additions are marked like this.
Line 1: Line 1:
조합. [Probability]공부의 기초 조합. [[Probability]]공부의 기초
Line 3: Line 3:
[Permutation]에서는 선택된 아이템들의 순서가 중요하다. [Combination]은 순서는 중요하지 않고, n개서 k개를 뽑아내는 가짓수이다. 이것역시 중복허용 조합과 중복비허용 조합으로 나뉜다. a,b,c에서 두개를 뽑는다고 하면, [[Permutation]]에서는 선택된 아이템들의 순서가 중요하다. [[Combination]]은 순서는 중요하지 않고, n개서 k개를 뽑아내는 가짓수이다. 이것역시 중복허용 조합과 중복비허용 조합으로 나뉜다. a,b,c에서 두개를 뽑는다고 하면,

조합. Probability공부의 기초

Permutation에서는 선택된 아이템들의 순서가 중요하다. Combination은 순서는 중요하지 않고, n개서 k개를 뽑아내는 가짓수이다. 이것역시 중복허용 조합과 중복비허용 조합으로 나뉜다. a,b,c에서 두개를 뽑는다고 하면,

중복없이 뽑을때 (without repetition)

$$ {n \choose k} = \frac{n!}{k!(n-k)!} = \frac{n(n-1) \cdots (n-k+1)}{1 \cdot 2 \cdots k} $$

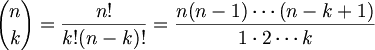
3!/2!= 3 즉 세가지 ab, ac, bc

중복을 허용해서 뽑을 때 (with repetition)

$$ {{n+k-1} \choose k} $$

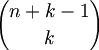
4!/(2!*2!) = 6 즉 여섯가지 aa, ab, ac, bb, bc, cc

조합과 관련된 수식들

$ {a \choose 0} = 1$, in particular, ${0 \choose 0} = 1$


$$ {n \choose k} = {n \choose {n-k}} $$ $$ {a \choose k} + {a \choose {k+1}} = {{a+1} \choose {k+1}} $$ $$ \sum_{s=0}^{n-1} {{k+s} \choose k} = {{n+k} \choose {k+1}} $$ $$ \sum_{k=0}^r {p \choose k} {q \choose {r-k}} = {{p+q} \choose r} $$

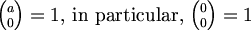
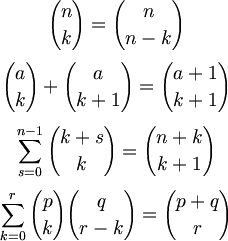
Python으로 구현하면

중복을 허용하지 않을때 

   1 def combo(aList, size=2): 
   2     if size==0 or not aList: 
   3         return [aList[:0]] 
   4     else: 
   5         result = [] 
   6         for i in range(0, (len(aList)-size)+1): 
   7             pick = aList[i:i+1] 
   8             rest = aList[i+1:] 
   9             for x in combo(rest, size-1): 
  10                 result.append(pick+x) 
  11         return result

보다 빠른 속도를 원한다면 ProbStat참고

SeeAlso http://aspn.activestate.com/ASPN/Cookbook/Python/Recipe/190465

Combination (last edited 2011-09-07 16:42:21 by 211)

web biohackers.net